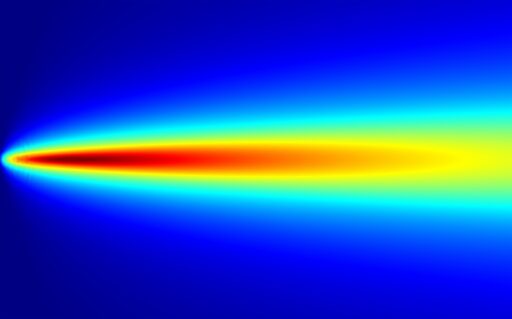
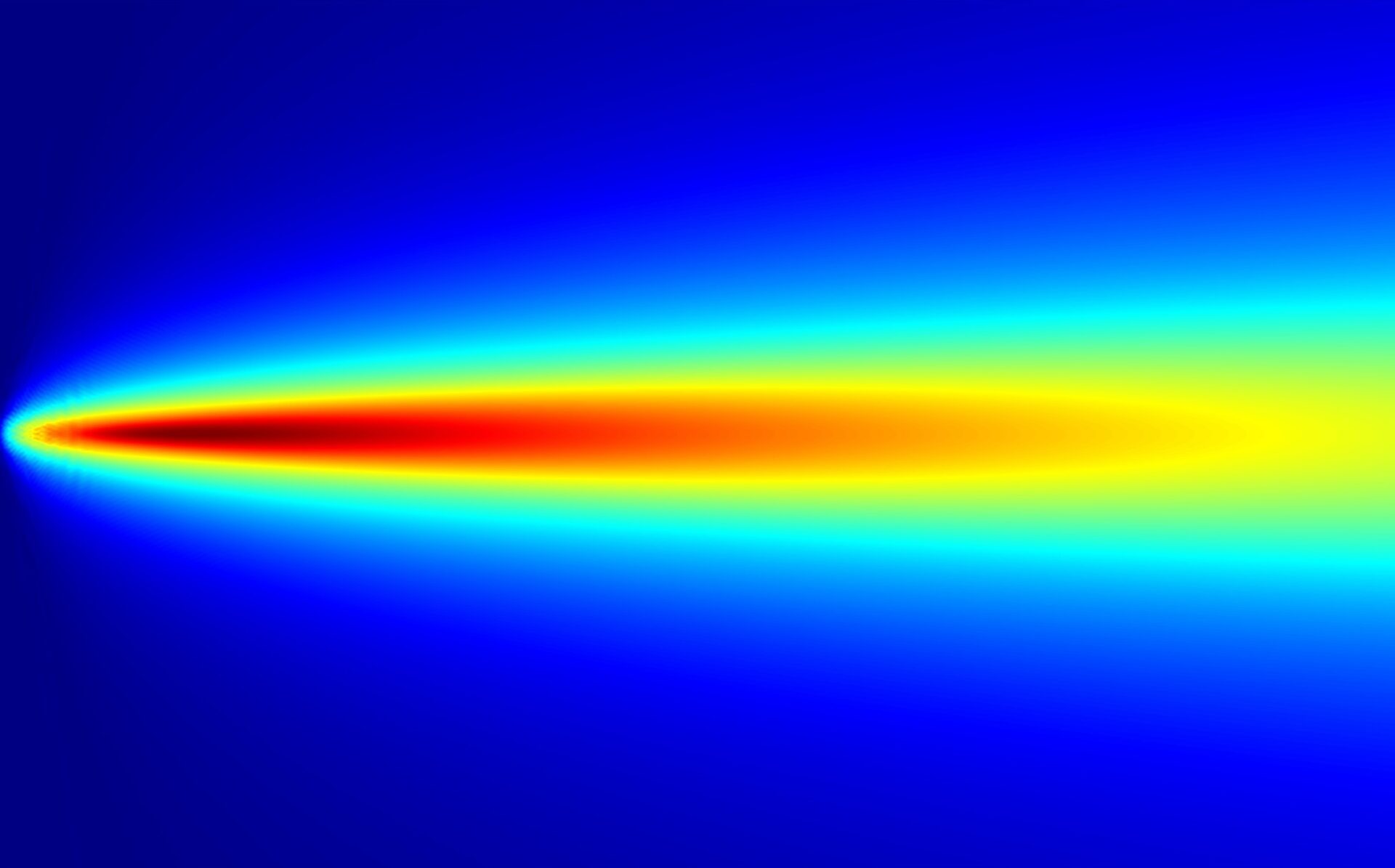
Audible sound (i.e., of low frequency) has weak attenuation (i.e., can propagate over long distances), but is also characterized by rapid divergence (i.e., are difficult to direct in a specific direction).
Ultrasonic waves (i.e., of high frequency), on the contrary, can have a pronounced directionality, but tend to rapidly attenuate in the propagation medium. However, at high power, two high-frequency waves are capable of nonlinear (parametric) interaction — generation of many additional harmonics (frequencies). In this case, the difference (lowest) frequency wave is narrowly directional and is able to propagate along a sufficient distance from the source, whereas the high-frequency waves quickly attenuate. Thus, inaudible ultrasound can generate, for example, audible sound that is directional and far-propagating.
Therefore, parametric generation of a difference-frequency wave is actively used in various applications:
- highly directional audible sound in the air (contactless audio guides in the libraries and museums, active noise control systems);
- highly directional signal that propagates over long distances in the water (profiling sea-bottom structures and long-range ocean research);
- medical applications (ultrasound difference-frequency imaging, contrast elastography), etc.
Such interaction of two high-frequency pump waves can be numerically calculated using the Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation. In this case, to perform three-dimensional calculations, it is necessary to optimize the algorithms by taking into account only the most significant spectral components of the nonlinear wave.
LIMU tasks
- Development of new numerical algorithms for solving three-dimensional parametric problems in highly nonlinear regimes
- Investigation of features of parametric difference-frequency wave generation
- Numerical calculations to define optimal characteristics of parametric sound radiation
- Development of specialized parametric sources for specific medical and industrial applications
Activity types
- numerical modeling
- transducer design
Contacts
Details
[1] Fully nonlinear three-dimensional modeling of parametric interactions in the field of a dual-frequency acoustic array / A. V. Kvashennikova, P. V. Yuldashev, V. A. Khokhlova, I. B. Esipov // Journal of the Acoustical Society of America. — 2024. — Vol. 155, no. 3. — P. 1682–1693. DOI: 10.1121/10.0025049
[2] Quasilinear approximation for modeling difference-frequency acoustic wave in a diffracting pump-wave beam / A. V. Tyurina, P. V. Yuldashev, I. B. Esipov, V. A. Khokhlova // Acoustical Physics. — 2023. — Vol. 69, no. 1. — P. 30–39. DOI: 10.1134/S1063771022700014
[3] Spectral modeling of difference-frequency generation in the case of two-frequency interaction of ultrasound waves / A. V. Tyurina, P. V. Yuldashev, I. B. Esipov, V. A. Khokhlova // Acoustical Physics. — 2022. — Vol. 68, no. 2. — P. 130–137. DOI: 10.1134/s1063771022020105
[4] Demodulation of pulsed acoustic signals in strongly nonlinear propagation regimes / A. V. Kvashennikova, M. S. Sergeeva, P. V. Yuldashev et al. // Acoustical Physics. — 2024. — Vol. 70, no. 5. — P. 797–807. DOI: 10.1134/s1063771024602279
[5] Parametric acoustic array and Its application in underwater acoustic engineering / H. Zhou , S. H. Huang, W. Li // Sensors (Basel). 2020 10;20(7):2148. DOI: 10.3390/s20072148.
[6] Development of parametric loudspeaker / C. Shi, G. Woon-Seng // IEEE Potentials. 2010 29: 20 – 24. DOI: 10.1109/MPOT.2010.938148